
#Special right triangles calculator 45 45 90 how to#
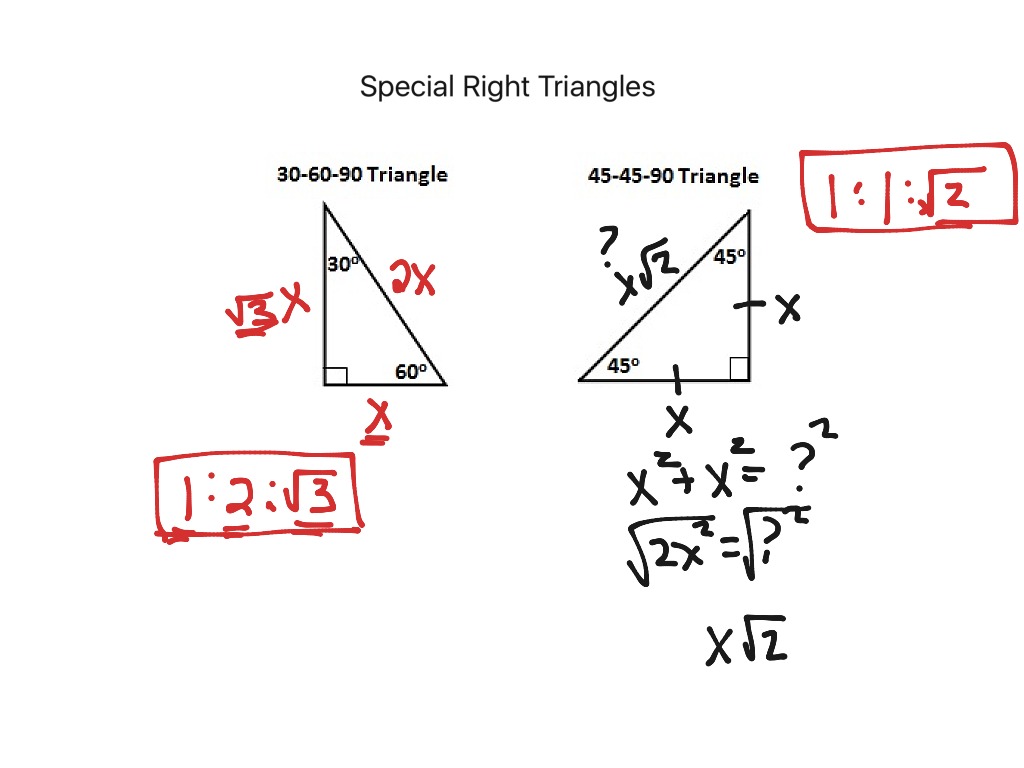
This video gives an introduction to the 45-45-90 triangles and shows how to derive the How to find the length of a leg or hypotenuse in a 45-45-90 triangle using the Pythagorean Theorem and then derive the ratio between the length of a leg and the hypotenuse? The following videos show more examples of 45-45-90 triangles. The third value of the ratio n:n:n√2 is 4√2 then the lengths of the other two sides must 4.Īnswer: The lengths of the two sides are both 4 inches. Step 2: You are given that the hypotenuse is 4√2. Step 1: This is a right triangle with a 45° so it must be In order to perform specific calculations regarding this type of triangle, you can take the support of different branches of mathematics including trigonometry. Is 4√2 inches and one of the angles is 45°. Triangle 30 60 90 Calculator This is a special right triangle having 30, 60, and 90 angles from all sides. If theįirst and second value of the ratio n:n:n√2 is 3 then the length of the third side is 3√2Īnswer: The length of the hypotenuse is 3√2 inches.įind the lengths of the other two sides of a right triangle if the length of the hypotenuse Step 2: You are given that the both the sides are 3. 30 60 90 and 45 45 90 Triangle Calculator. 45 45 90 Special Right Triangle Calculator, 30 60 90 Special Right Triangle Calculator, How to Calculate Edge Lengths of an Isosceles Triangle, How to. 30 60 90 triangles three angles measure 30. Step 1: This is a right triangle with two equal sides so it A 30-60-90 right triangle is a special type of right triangle.
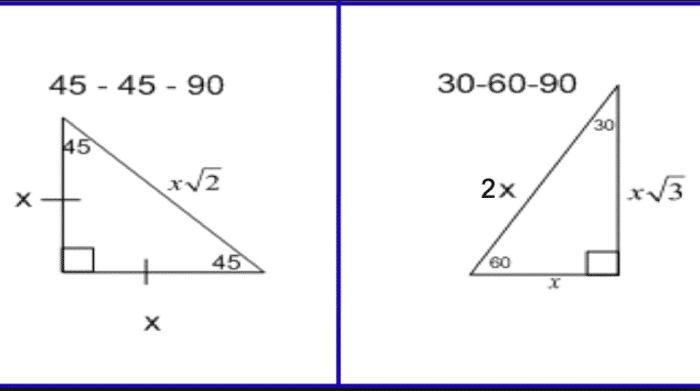
How to solve problems with 45-45-90 triangles?įind the length of the hypotenuse of a right triangle if the lengths of the other two sides are both 3 inches. Of the angles in the right-angle triangle is 45° then it must be a 45-45-90 special right triangle.Ī right triangle with a 45° angle must be a 45-45-90 special right triangle. You can also recognize a 45-45-90 triangle by the angles. It is also sometimes calledĪ right triangle with two sides of equal lengths is a 45-45-90 triangle. Note that a 45-45-90 triangle is an isosceles right triangle. The page for more examples and solutions using the 45-45-90 triangle. The following diagram shows a 45-45-90 triangle and the ratio of its sides. It is a special triangle because its side lengths are always in the ratio of 1:1: 2 (x: x: x2 for side1: side2: hypotenuse). It is also sometimes called an isosceles right triangle since it has two equal sides and two equal angles. Lengths of the sides of a 45-45-90 triangle are in the ratio of 1:1:√2. A 45-45-90 triangle is a special right triangle that has two 45-degree angles and one 90-degree angle. What is a 45-45-90 Triangle? Ī 45-45-90 triangle is a special right triangle whose angles are 45°, 45° and 90°. Special triangle it can save you some calculations. Pythagorean theorem formula, but if you can see that it is a A special right triangle is a right triangle Provide a shortcut when answering some questions. However, the methods described above are more useful as they need to have only one side of the 30 60 90 triangle given.Recognizing special right triangles in geometry can the sine and cosine of 30° to find out the others sides lengths:Īlso, if you know two sides of the triangle, you can find the third one from the Pythagorean theorem.
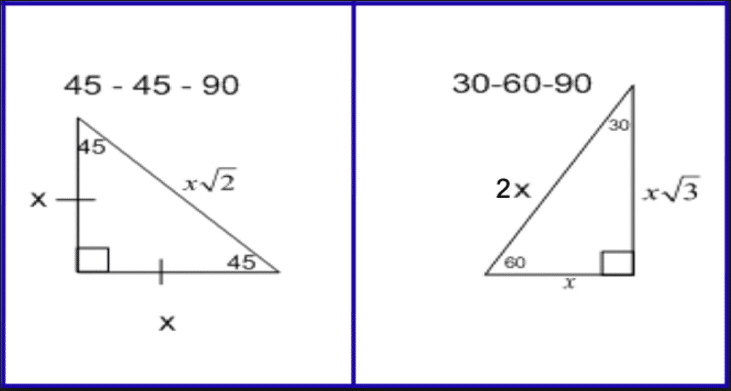
If you are familiar with the trigonometric basics, you can use, e.g. It's equal to side times a square root of 3, divided by 2: Using the properties of the equilateral triangleĭid you notice that our triangle of interest is simply a half of the equilateral triangle? If you remember the formula for the height of such a regular triangle, you have the answer what's the second leg length.The formulas are quite easy, but what's the math behind them? Let's check which methods you can use to prove them: How to solve a 30 60 90 triangle? 30 60 90 triangle formulaĪssume that the shorter leg of a 30 60 90 triangle is equal to a.


 0 kommentar(er)
0 kommentar(er)
